Simple Mathematics Proposed in this Blog

This blog proposes a mathematical basis for measuring a country’s proximity to a goal of achieving an ideal healthcare system. For this purpose, this blog proposes a scoring system called the 6P score. In addition, it proposes a multivariate regression that will establish the relative importance of each of the six principles describing an ideal healthcare system through the computation of regression coefficients. These will help policymakers guide investments in healthcare to derive the best bang for the buck so that at the margin, each dollar is spent on a variable that yields the best improvement in HALE.

In summary,

1. We start with 6 basic variables that define an ideal healthcare system.

2. We collect data on these 6 variables from established WHO databases.

3. We collect data on HALE.

There are several epidemiological variables other than these six that may affect HALE for a country. For example, if the average age of the population is advanced, the HALE by definition, would be skewed accordingly as the elderly may have shorter intervals of healthy periods of life compared to a decidedly younger population. Second, the presence of a sweeping disease epidemic in a country would alter HALE. Third, the presence of wars or catastrophic events can also alter reported HALE.

If for every country denoted by , each attribute denoted by is allotted a weight of such that . The weight is the same across all countries . Let the value of each attribute for country be . This value is the amount each country has invested in the attribute .   may be a PPP dollar amount or a rank order or a binary yes/no variable. Then the weighted average 6P score is:

(1)  

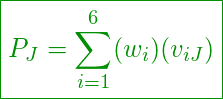
How to estimate the relative attribute weights 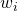? – A multivariate regression

The weights are estimated using current data on these attributes. A multivariate regression can be run with the six attributes and three epidemiological variables as the independent variables and, say, HALE as the dependent variable. The resulting coefficients, for the six variables normalized to a total of 1 become the weights.

The regression equation would then be:

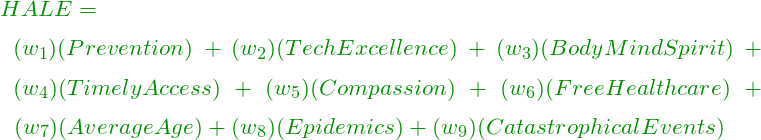
where are the respective coefficients.

By its very nature, multivariate regression has several underlying assumptions:

In our instance, we will have to check to ensure that these assumptions are upheld. Our independent variables must especially be checked for multicollinearity and autocorrelation. Statistical tests are available to check for these assumptions.

The Next Steps

The next six posts will describe the nature of data for each of the six principles. They will discuss the pitfalls and methods used to interpret and collect data on the six components. Once data is collected for all six components together with the three epidemiological variables affecting HALE, the multivariate regression can be run with HALE as the independent variable and the aforementioned nine variables as dependent. The coefficients of the six variables characterizing an ideal healthcare can next be normalized to a total of 1 thus yielding weights for each of the six attributes.

Results

Using the results of the regression above with normalized weights for each of the six attributes, one can calculate the 6P score using the formula (1) above and rank countries in their closeness to an ideal healthcare system.  One can also calculate the correlation between these weights and HALE. This identifies those attributes that are significant contributors to population health measured by HALE.

What does all this mean?

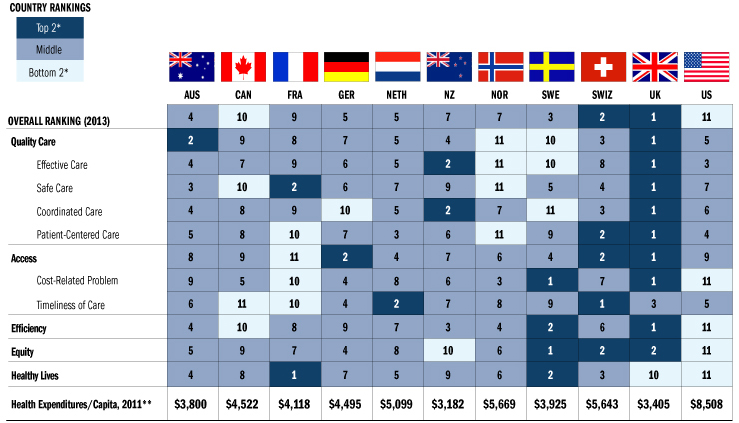
As an illustration of the technique, let us consider the 11 countries listed in the OECD report below taken from K. Davis, K. Stremikis, C. Schoen, and D. Squires, Mirror, Mirror on the Wall, 2014 Update: How the U.S. Health Care System Compares Internationally, The Commonwealth Fund, June 2014. The table below is taken directly from their paper.

Consider the following attributes: Effective Care (presumed proxy for state-of-the-art), Patient Centred Care (presumed proxy for compassionate care), Access (presumed proxy for timely access), Healthy Lives (presumed proxy for disease prevention). We do not have data on actual expenditures at this moment in this Table. However, we can apply our calculations to the ordinal rankings. Please see a good discussion of this technique in Optimum Studia Ekonomiczne, 5(65), 14-33, 2013. Please also note that because we are using ranks to calculate the aggregate weight adjusted scores for each country, the final ranking will be dependent on the initial ranking and the cohort.

The following Table summarizes the results. Please note that the country rankings can potentially change because of the relative weights assigned to the attributes.

Weight Adjusted Country Rank

Attribute (Weight)	USA	UK	SWZ	SWE	AUS	GER	NET	NZL	NOR	FRA	CAN
Effective (0.3)	0.9	0.3	2.4	3.0	1.2	1.8	1.5	0.6	3.3	2.7	2.1
Patient Centred (0.4)	0.8	0.2	0.4	1.0	1.0	1.4	0.6	1.2	2.2	2.0	1.6
Access (0.2)	1.8	0.2	0.4	1.6	1.6	0.4	0.8	1.4	1.2	2.2	1.8
Healthy Lives (0.3)	3.3	3.0	0.9	1.2	1.2	2.1	1.5	2.7	1.8	0.3	2.4
Overall Score	6.8	3.7	4.1	6.2	5.0	5.7	4.4	5.9	8.5	7.2	7.9
New Ranking	9	1	2	7	4	5	3	6	11	8	10

This Table shows an example of why the weight adjusted rankings can differ from raw rankings depending upon the weights used. In practice these weights would be calculated based on the results of a multivariate analysis described above.

What do we need to do?

We need to collect data on expenditures, rankings or binary answers (dummy variables) on the six principles (attributes), and three epidemiological variables and HALE for each country. Next, we need to run a multivariate regression using this data. Then, we obtain the relative weights normalized to 1 for the six variables from the result of the regression analysis. Finally, we use these weights to compute the 6P score for each country, the adjusted weighted rankings of countries in how they measure up to an ideal healthcare system and the marginal contribution of each attribute to the country’s HALE.